Polarization

You can plot a particular polarization in both 2D and 3D patterns. For a 2D pattern, the polarization is a property of the curve and may be changed by selecting Graph > Manage Curves and selecting the desired polarization in the Measurement section. For a 3D pattern, the polarization is a property of the graph and may be changed by selecting Graph > Graph Options : [Polarization]. The types of polarization available are described below.

Theta-Phi

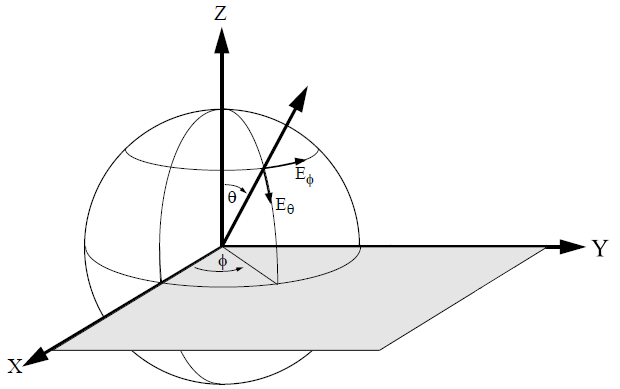
You may choose between E-Total, E-Theta, or E-Phi, where E-Total is the vector sum of two polarization components, E-Theta (Εθ) and E-Phi (Εϕ), as shown in the figure describing spherical coordinates below. Close to the horizon, theta polarization corresponds to vertical polarization, while phi polarization corresponds to horizontal polarization.

Circular

For circular polarization, the left-hand circular polarized (E-LHP) component and the right-hand circular polarized (E-RHP) component of the electric field can be displayed. The Axial Ratio of the electric field is the ratio of the magnitudes of the major to the minor axis.

Most polarized antennas require you to set the phase of your ports, which can be setup when you first open your Pattern tab.  You may also edit your port phases at any time by selecting Graph > Calculations or clicking the Calculations button .

Ludwig-3

Ludwig-3 is an abbreviation for Ludwig’s third definition of polarization and cross-polarization1. This definition allows the analysis of polarization and cross-polarization in much the same manner as it is often measured. Therefore, the two components are co-polarization (Co-Pole) and cross-polarization (Cross-Pole).

Ludwig Angle: To use Ludwig-3, you need to enter a reference angle, in degrees. This angle is the angle of the polarization at beam center. Thus, at beam center there is zero cross-polarization.

A detailed description of Ludwig-3 is beyond the scope of this topic. More detail is available in the original reference1.

A. C. Ludwig, "The Definition of Cross Polarization,” IEEE Trans. Ant. and Prop., January, 1973, pp. 116 - 119.