EM Solvers
Sonnet provides two solvers. Both solvers use the method of moments. The Direct Solver is Sonnet’s traditional solver and has been used for decades. The Beowulf Solver is a new, O(N log N) fast solver which is designed to be more efficient for large circuits. Both solvers operate on the same geometry and same project files, and both get the same results to a specified precision. However, they go about the solution in very different ways. See Sonnet References for published papers describing the algorithms used by Sonnet.
By default, the Direct Solver is used. If you wish to use the Beowulf Solver, you may manually change the setting in your project by following these steps:
Select Circuit > Settings > [EM Options].
Click on > Advanced to expand the advanced section of the dialog box.
Click the Beowulf sub-tab.
Select Beowulf Solver from the Matrix Solver drop-down list.
A Beowulf license is required to use the Beowulf solver.
Direct Solver
Method of moments solvers are very elegant in that they are generally just solving Ohm’s law, albeit in the frequency domain.
V = I R
It can also be written in matrix form.
[Z] [I] = [V]
The Direct Solver then takes all the interactions across N subsections, which yields an N x N matrix of interactions. [V] is the port excitations, and [I] is the current being solved for. The solution is found by factorizing the [Z] matrix, which effectively moves it to the right side of the equation, making the solution trivial.
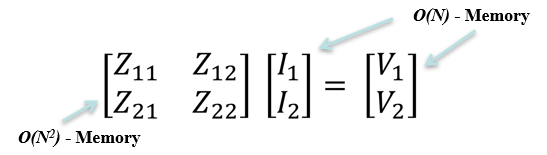
This method has the advantage of being direct, which is predictable in performance and full precision. It is preferred whenever performance limitations do not prohibit usage, which typically means small and medium-complexity circuits.
Beowulf Solver
The name Beowulf comes from an Old Norse epic poem; the titular character was known for protecting his community by handling very large monsters, much like how the Beowulf Solver can handle very complex electromagnetic problems.
Beowulf is an iterative method. It does not attempt to factorize the matrix, rather, it optimizes the solution through several attempts. During each attempt, the [I] vector is assumed, and a matrix-vector product is calculated. The result is compared to the port excitations, with the difference being a residual error representing the present error of the solution.
This process happens inside the Fourier domain, using a lossless compression algorithm to store the matrix, part of the United-FFT method. This is unique in that iterations can proceed to full numerical precision; no accuracy nor precision needs to be traded for the better scaling of the algorithm.
This does, however, have downsides. First, there is overhead to setting up this process, so very small circuits will take longer to run. Second, the number of iterations is not known beforehand, so performance can potentially be difficult to gauge. Therefore, Beowulf is recommended for use only when the required resources to simulate using the Direct Solver are either impractical or unavailable, which typically means very complex circuits.
Paradigm Shifts Moving from the Direct to the Beowulf Solver
- In Beowulf, the number of subsections is relatively unimportant; since there is no explicit matrix, there is also no matrix to grow in size.
- In general, the Beowulf Solver should use less memory than the Director Solver for large circuits. However, sometimes it may use more. The memory increases with:
- The number of cells in the box (2 * N * M)
- The number of planes (P^2)
- The weight of the preconditioner
- The Beowulf Solver requires selection of a preconditioner and of a precision. Sonnet uses default settings for reasonable performance across most cases. However, advanced users may wish to override these default settings.
Preconditioners
Preconditioners are a way to make the Beowulf Solver converge faster. Fewer matrix vector multiplies are necessary with a better and heavier weighted preconditioner. But the heavier the preconditioner is, the more time it takes to solve before the matrix-vector multiplies can converge, and the more memory required. The default preconditioner is Cloud/Medium. In general, Sonnet’s Cloud/Medium preconditioner should provide reasonable performance. However, Cloud/Large can be selected to speed convergence in exchange for more pre-compute time and memory. Cloud/Small can be selected to reduce memory requirements but increase simulation time. In extreme cases--typically electrically very large structures like antenna arrays--EDAG/Mini can be used effectively. You may set the preconditioner used by the Beowulf Solver by selecting it from the Preconditioner drop-down list.
Precision
The precision selection tells Beowulf when to stop iterating, and reflects the number of significant figures that have been calculated in the simulation with respect to the Real and Imaginary components of the S-Parameters in absolute terms (as opposed to dB). This can be set by the user to balance speed and accuracy. The default is 6 significant figures which represents a full single-precision simulation. Up to 12 can be specified for a full double precision simulation. As few as 2 can be selected, however this can be dangerous as it is a large degree of error. You may change the precision by entering it in the Precision section of the Beowulf tab.
Features Not Support by the Beowulf Solver
The following features are not supported by the Beowulf Solver:
- Conformal Mesh: Any polygons using the Conformal Mesh meshing model will be reverted to Rectangular Mesh.
- TrueVolume: If a circuit contains any TrueVolume polygons, the Beowulf Solver will issue an error message and exit.
- Dielectric Bricks: If a circuit contains any Dielectric Brick polygons, the Beowulf Solver will issue an error message and exit.
- Symmetry: If a circuit uses Symmetry, the Beowulf Solver will issue an error message and exit.
- Single and Quad Precision: The Precision settings in the Analysis Options tab of the EM Options pane are ignored by the Beowulf solver. The Beowulf Solver calculations are always performed in double-precision.