Benchmarking
Evaluation of Electromagnetic Software
Revised: June 4, 1997
© Copyright 1994, 1999 Sonnet Software, Inc. All Rights Reserved
Table of Contents
Chapter 1 - Introduction
Chapter 2 - Technical Overview
Chapter 3 - The Stripline Standard
Chapter 4 - The Stripline Standard and Triangular Subsections
Chapter 5 - The Microstrip Standard
Chapter 6 - The Coupled Microstrip Standard
Chapter 7 - Limit Tests
Chapter 8 - Lossy Ground Plane and Lossy Dielectric Tests
Chapter 3 - The Stripline Standard
Specific Analysis Information | References
Since zero thickness lossless stripline has an exact theoretical solution, it is ideal for use as a benchmark for evaluation of electromagnetic analyses. Described here is one of several standard striplines we have investigated. This particular standard stripline has been published in [1] (from which this chapter is adapted) and [2]. To within the indicated tolerances, this line is precisely 50 Ohms and the line length is exactly 90 degrees at 15 GHz. The ground plane spacing allows single mode propagation up to about 100 GHz.
The fundamental idea of the standard stripline is that we know exactly what the correct answer is, thus, we can easily calculate what the exact error is in an analysis of the standard stripline.
Note that Sonnet users can obtain a geometry file describing the Stripline Standard at 16 cells wide and 128 cell long by clicking on Sonnet -> Copy Examples and typing the command "copyex s50.geo". This will copy the geometry file into the project directory.
We have included a form, Figure 1, to encourage consistent reporting of results. The first column, labeled "N", allows specification of an analysis specific parameter. We call it the discretization parameter. For example, for subsectional based analyses, we have found that the number of cells into which the width of the line is divided is of primary importance for analysis accuracy. Whatever discretization parameter is chosen, we recommend performing the analysis over a range of the parameter which allows increased accuracy while, presumably, also requiring increased analysis time. Report the value of the selected discretization parameter (e.g., cells per width), in the first column of the table. Since different analyses may use different discretization parameters, this parameter should not be used for comparison purposes. It should be provided (along with the information in the table entry "Other Analysis Param.:") to allow independent researchers to duplicate the results.
The next two columns are for S11 magnitude and S21 angle. Since the correct value of S11 magnitude is zero, any difference from zero is error. At 15 GHz, the correct value of S21 phase is -90 degrees. Again, any difference is error.
Next, calculate the error using the equation specified in the form.
The final two columns report the time required. The first time column is for actual analysis time. Some analyses now place the portion of the analysis which is independent of the specific circuit geometry in a separate "pre-computation" analysis. Thus, we have included a column for reporting pre-computation time. Neither should the pre-computation time be included with the analysis time, nor should it be left un-reported. It is also useful to provide a plot of analysis time versus accuracy. For consistency, we suggest plotting Error (%) on the vertical axis and Time (Seconds) on the horizontal axis using a log-log grid.
Results for Sonnet, Version 2.4 are shown in Figure 2 and Figure 3. The discretization parameter is cells per line width, which ranges from 1 to 512 cells per line width. Since variable size subsections (in terms of the cell size) are used, there are actually fewer than 512 subsections per line width. The line is divided into 128 cells along its length for all cases. This is why the S21 phase is nearly constant. Faster results with nearly the same accuracy can be obtained if the line length is divided into only 64 or even as few as 32 cells.
Figure 2 shows the numeric Sonnet results. These results are plotted in Figure 3. We see that the 1% error level is reached with just over 10 Seconds of HP-710 (a low end HP-700) analysis time. An error of 0.1% is reached after about 200 Seconds of analysis time. The 0.05% error level is reached with 30 minutes of analysis time. At this point the line length should be divided into more than 128 cells to continue realizing reduced error.
Using the Stripline Standard, we can empirically derive an expression for the Sonnet analysis error due to subsection size. The result is:
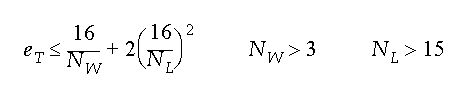
where NW is the number of cells across a line width (transverse to current flow) and NL is the number of cells per wavelength (parallel to current flow) and eT is the error in percent. It is likely that this same expression estimates the error due to subsectioning for any method of moments program which uses roof-top basis functions.
Error in the 10% range is unacceptable for most engineering applications. A range around 1% may be the most commonly required level, yielding a high probability of success on first fabrication. In a few very rare cases, 0.1% may be desired.
The most important shortcoming of this standard is that it does not test dispersion. Lossless stripline operated in the fundamental TEM mode, has no dispersion. On the other hand, being dispersionless, there is no uncertainty as to the characteristic impedance. Even with these limitations, this stripline standard allows the precise quantitative investigation of the accuracy of a large number of 3-D planar electromagnetic analyses at error levels never before considered feasible.
Media: Stripline
Frequency: 15 GHz. If other frequencies are analyzed, the line length, L, should be changed to maintain a quarter wavelength. Otherwise, the given error equation is invalid.
Ground plane spacing: B = 1.0 mm, exactly.
Substrate dielectric constant: 1.0, exactly.
Line width: W = 1.4423896 mm +/- 1.0 x 10-8.
Line length: L = 4.99654097 mm +/- 1.0 x 10-9.
Sidewalls: If present, place more than 5 mm from line edges.
Conductor thickness: 0.0 mm, exactly.
Conductor and dielectric loss: Lossless.
Analysis range: For subsectional analyses, recommend analysis at 1, 2, 4, 8, 16, etc. cells wide. For other kinds of analyses, if possible, vary critical discretization parameters for increasing accuracy.
| N | Mag(S11) | Ang(S21) | Error(%) | Analysis Time (Sec) | Pre-comp. Time (Sec) |
| Analysis Tool (Name/Version): | |
| Description of "N": | |
| Other Analysis Parameters: | |
| Frequency (GHz): | 15.0 GHz |
| Computer / RAM: | |
| Date: | |
| Performed by (Name): | |
| Performed by (Company): |

| N | Mag(S11) | Ang(S21) | Error(%) | Analysis Time (Sec) | Pre-comp. Time (Sec) |
| 1 | 0.05895 | -89.999 | 5.90 | 1 | 0 |
| 2 | 0.05895 | -89.999 | 5.90 | 1 | 0 |
| 4 | 0.03530 | -89.999 | 3.53 | 3 | 0 |
| 8 | 0.01958 | -89.998 | 1.96 | 7 | 0 |
| 16 | 0.01026 | -89.999 | 1.03 | 14 | 0 |
| 32 | 0.00526 | -90.000 | 0.52 | 30 | 0 |
| 64 | 0.00266 | -90.000 | 0.27 | 66 | 0 |
| 128 | 0.00138 | -90.005 | 0.14 | 157 | 0 |
| 256 | 0.00066 | -90.009 | 0.07 | 491 | 0 |
| 512 | 0.00036 | -89.983 | 0.05 | 1969 | 0 |
| Analysis Tool (Name/Version): | Sonnet / Version 2.4 |
| Description of "N": | Cells per line width |
| Other Analysis Parameters: | Line 128 cells long, Var. sub. size |
| Frequency (GHz): | 15.0 GHz |
| Computer / RAM: | HP-710 / 64 Mbytes |
| Date: | 12 October 1993 |
| Performed by (Name): | J. Rautio |
| Performed by (Company): | Sonnet Software, Inc. |

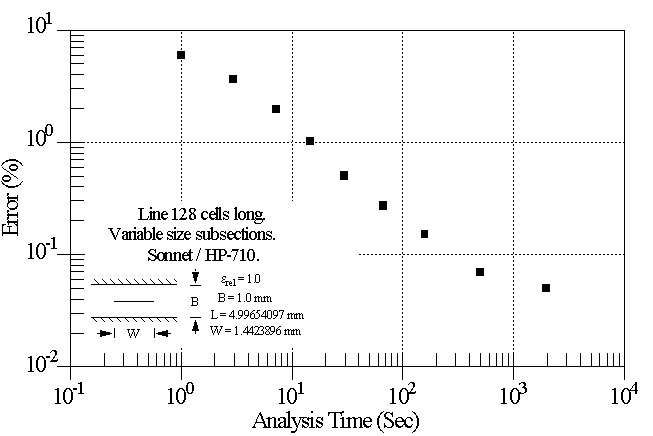
Figure 3. The analysis time versus percent error plot for Sonnet shows the critical 1% point passed with just over 10 Seconds of execution time.
[1] J. C. Rautio, "MIC Simulation Column - A Standard Stripline Benchmark," International Journal of Microwave & Millimeter-Wave Computer-Aided Engineering, Vol. 4, No. 2, April 1994, pp. 209-212.
[2] J. C. Rautio, "An Ultra-High Precision Benchmark For Validation Of Planar Electromagnetic Analyses," IEEE Tran. Microwave Theory Tech., accepted for publication.
[3] J. C. Rautio, "An Investigation of an Error Cancellation Mechanism with Respect to Subsectional Electromagnetic Analysis Validation," International Journal of Microwave and Millimeter-Wave Computer-Aided Engineering, Vol. 6, No. 6, November 1996, pp. 430-435.
[4] J. C. Rautio, "The Microwave Point of View on Software Validation," IEEE Antennas and Propagation Magazine, Vol. 38, No. 2, April 1996, pp. 68-71.
[5] J. C. Rautio, "EM-Analysis Error Impacts Microwave Designs," Microwaves and RF, September 1996, pp. 134-144.
[6] J. C. Rautio, "A Precise Benchmark for Numerical Validation," IEEE International Microwave Symposium, Workshop WSMK Digest, Atlanta, June 1993.
[7] J. C. Rautio, "Response #3. Standard Stripline Benchmark - MIC Simulation Column," International Journal of Microwave and Millimeter-Wave Computer-Aided Engineering, Vol. 5, No. 5, September 1995, pp. 365-367.
[8] J. C. Rautio, "Response #2. Comments on Zeland's Standard Stripline Benchmark Results - MIC Simulation Column," International Journal of Microwave and Millimeter-Wave Computer-Aided Engineering, Vol. 5, No. 6, November 1995, pp. 415-417.
[9] J. C. Rautio, "Characterization of Electromagnetic Software," 42nd ARFTG Conference Digest, San Jose, CA, Dec. 1993, pp. 81-86.
[10] J. C. Rautio, "Some Comments on Electromagnetic De-Embedding and Microstrip Characteristic Impedance" International Journal of Microwave & Millimeter-Wave Computer-Aided Engineering, Vol. 3, No. 2, April 1993, pp. 151-153.
[11] J. C. Rautio, "Experimental Validation of Electromagnetic Software," International Journal of Microwave & Millimeter-Wave Computer-Aided Engineering, Vol. 1, No. 4, Oct. 1991, pp. 379-385.
[12] J. C. Rautio, "A New Definition of Characteristic Impedance", MTT International Symposium Digest, June 1991, Boston, pp. 761-764.
[13] J. C. Rautio, "Experimental Validation of Microwave Software," 35th ARFTG Conference Digest, Dallas, May 1990, pp. 58-68. (Voted best paper at the conference.)
On to Chapter 4 - The Stripline Standard and Triangular Subsections



