Benchmarking
Evaluation of Electromagnetic Software
Revised: June 4, 1997
© Copyright 1994, 1999 Sonnet Software, Inc. All Rights Reserved
Table of Contents
Chapter 1 - Introduction
Chapter 2 - Technical Overview
Chapter 3 - The Stripline Standard
Chapter 4 - The Stripline Standard and Triangular Subsections
Chapter 5 - The Microstrip Standard
Chapter 6 - The Coupled Microstrip Standard
Chapter 7 - Limit Tests
Chapter 8 - Lossy Ground Plane and Lossy Dielectric Tests
Chapter 8 - Lossy Ground Plane And Lossy Dielectric Tests
Ground Plane Loss Test | Results For Ground Plane Loss | Dielectric Bulk Conductivity Test |
The first test of this benchmark uses two nearly identical capacitors which should give nearly identical results. The capacitors are formed with identical top plates a very small distance above a ground plane. Thus, the ground plane forms the bottom plate of the capacitors. In both cases, loss is present only in the ground plane. The two capacitors are different in that the ground plane of one is formed from regular subsectioned metal while the other is formed from the bottom cover of the box.
The second test (which uses Test Structure C), uses loss only in the capacitor dielectric. The loss used creates a 50 Ohm resistor. Difference in the resistance from 50 Ohms is error in the evaluation of dielectric loss.
Failure of an analysis to pass either test at the desired level of error is sufficient to conclude that the analysis is inappropriate for use at that error level for the analysis of ground plane loss (first test) or dielectric loss (second test).
Ground plane loss is important when magnetic current subsections are used to simulate gaps in a ground plane. Gaps in a ground plane might be used to simulate coplanar waveguide or slot line. If the ground plane loss is incorrect, then the coplanar waveguide loss calculation is also incorrect.
As for microstrip, most of the microstrip loss is in the microstrip conductor. But there is also some loss in the microstrip ground. Thus if ground plane loss is underestimated, then microstrip loss is underestimated.
This is also a problem for high speed digital. If the ground is a perfect conductor, "ground bounce" and "ground loops" can not happen. If loss is not calculated correctly, then ground bounce and ground loops are not calculated correctly.
Ground plane loss and dielectric loss, unlike normal conductor loss, require the calculation of a complex (i.e., real and imaginary) Green's function. In contrast, loss in subsectioned circuit metal does not require a complex Green's function.
Since ground plane loss requires a modified Green's function, there is a chance that bugs or numerical errors might cause incorrect results. This test is based on two different models of the same capacitor. In both cases, the capacitor is formed with normal subsectioned metal forming a lossless top plate. The bottom plate of the capacitor is a ground plane. In Test Structure A, the ground plane is formed from normal subsectioned metal, a so-called "artificial" ground plane. The metal of the artificial ground plane is lossy. In this case, the usual analysis ground plane (bottom cover of the box) is moved far from the capacitor so that it has no influence. Even though the analysis ground plane has no influence on Test Structure A, it should be lossless so that a complex Green's function is not calculated.
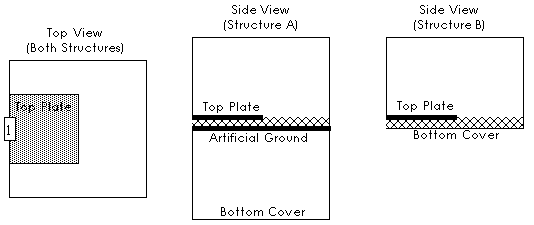
Figure 14. Top and side views of both test structures. In structure A, the lossy ground plane is composed of regular subsectioned metal. In structure B, the box bottom cover forms the lossy ground plane. Results from each should be nearly identical.
The bottom plate of the capacitor in Test Structure B uses the ground plane usually used in the analysis (i.e., the box ground plane or bottom cover). Subsectioned metal is not used for the ground plane. This means that 1) No subsections are used for the ground plane, and 2) A complex Green's function must now be calculated.
Both structures should give close to the same result, the only difference being due to the difference between a subsectioned ground (in Test Structure A) and the usual analysis ground plane (used in Test Structure B).
Important parameters for the test structures are summarized below.
| Table 3: Test Structure A Important Parameters | |
| Parameter | Value |
| Type of Structure | Thin dielectric capacitor connected in shunt to ground. |
| Ports | One port, along one side of the square capacitor. |
| Connecting transmission line length | 0 (not critical). |
| Capacitor Placement | Along one edge of the substrate, for port attachment. |
| Capacitor Top Plate | Normal subsectioned metal. |
| Capacitor Bottom Plate | Normal subsectioned metal covering entire substrate surface. |
| Dielectric Thickness | 0.1 micron (not critical). |
| Dielectric Constant | 10.0 (not critical). |
| Capacitor Area | 0.5 x 0.5 mm (not critical). |
| Substrate Size | 1.0 x 1.0 mm (not critical). |
| Frequency of Analysis | 10 GHz (not critical). |
| Cell Size | So substrate is 8 x 8 cells (not critical). |
| Top Plate Resistance | Lossless (critical). |
| Bottom Plate Resistance | 10.0 Ohms/square, frequency independent (large value means more sensitive to loss error, must be same as Box Ground Plane Loss in Test Structure B.) |
| Ground Plane Resistance | Lossless (ground plane positioned far from the capacitor). |
| Table 4: Test Structure B -- Important Parameters | |
| Parameter | Value |
| Capacitor Bottom Plate | Box ground plane. |
| Box Ground Plane Loss | 10.0 Ohms/square, frequency independent (must be same as Bottom Plate Resistance in Test Structure A.) |
| All Other Parameters | Identical to test structure A. |
Analysis of both structures with Sonnet Version 4.0 yields the following results:
| Table 5: Results With Lossy Subsectioned Metal (A) and With Lossy Ground Plane (B) | ||
| S11 (mag) | S11 (ang) | |
| Structure A | 0.9700 | -179.4 |
| Structure B | 0.9704 | -179.4 |
For unknown reasons, when a smaller subsection size is used, the difference between the two structures increases slightly as we see in the following data for which the cell size has been cut in half (the substrate is now 16 x 16 cells):
| Table 6: Results With Cell Size Cut In Half | ||
| S11 (mag) | S11 (ang) | |
| Structure A | 0.9743 | -179.0 |
| Structure B | 0.9748 | -178.9 |
Dielectric Bulk Conductivity Test
This test is based on a slightly modified version of the above capacitor structure. Strictly speaking, it tests only for bulk conductivity error. However, since loss tangent is exactly equivalent to a frequency dependent bulk conductivity, this test is likely to be sensitive to loss tangent modeling error as well. This test is most easily performed with Sonnet 4.0 or higher where bulk conductivity can be directly specified for each dielectric layer.
| Table 7: Test Structure C -- Important Parameters | |
| Parameter | Value |
| Capacitor Dimensions | 0.5 x 0.5 mm (same as before, but now critical). |
| Dielectric Bulk Conductivity | 0.008 S/M (critical). |
| Dielectric Constant | 1.0 (not critical). |
| Cell Size | So substrate is 64 x 64 cells (not critical). |
| Ground Plane Resistance | Lossless (Critical). |
| All Other Parameters | Identical to test structure B. |
The given bulk conductivity makes the structure behave as a 50 Ohm resistor to within the degree allowed by the cell size. The magnitude of S11 should approach zero as the analysis frequency approaches zero. Any difference is error. Sonnet provides the following results:
| Table 8: Sonnet results for the dielectric loss test. | ||
| Frequency | S11 (mag) (no de-embedding) | S11 (mag) (with de-embedding) |
| 1 GHz | 0.96133 | 0.96122 |
| 1 MHz | 0.00405 | 0.00369 |
| 1 kHz | 0.00206 | 0.00122 |
| 1 Hz | 0.00206 | 0.00122 |
At 1 GHz, the capacitor dominates, creating a short circuit. Without de-embedding, S11 magnitude converges to 0.002 which means the calculated resistance is in error by 0.4%. A portion of that error is due to the lack of de-embedding. With de-embedding, the error decreases to 0.24%.
The equivalent circuit of the structure is a capacitor and resistor in parallel. The resistor should be 50 Ohms. Any difference is error. De-embedding removes only second order error because the port discontinuity is almost purely capacitive and simply increases the value of the total capacitance, it has little effect on the resistance of the equivalent circuit. Sonnet's SPICE lumped model synthesis option was used to generate the equivalent circuit (analysis at two frequencies required). Alternatively, one could also simply invert the real part of the calculated Y-Parameter. Sonnet provides the following results:
| Table 9: Sonnet SPICE model synthesis results for the dielectric loss test (no de-embedding). | |
| Frequencies for SPICE model synthesis | Resistance (Ohms) |
| 1 and 1.1 GHz | 49.786 |
| 1 and 1.1 MHz | 49.795 |
| 1 and 1.1 kHz | 49.795 |
| 1 and 2 Hz | 49.795 |
The convergence seen here is due to the increasing validity of a lumped model at lower frequency. A frequency of 2 Hz was used for the last analysis because Sonnet does not allow a difference of 0.1 Hz between two frequencies.
Note that this approach has also converged to the same 0.4% error.
We repeated the analyses with de-embedding. Sonnet now provides the following results:
| Table 10: Sonnet SPICE model synthesis results for the dielectric loss test (with de-embedding). | |
| Frequencies for SPICE model synthesis | Resistance (Ohms) |
| 1 and 1.1 GHz | 49.870 |
| 1 and 1.1 MHz | 49.878 |
| 1 and 1.1 kHz | 49.879 |
| 1 and 2 Hz | 49.878 |
The error is now 0.24%, consistent with the previous de-embedded results.



